Correspondance en coordonnées sphériques:
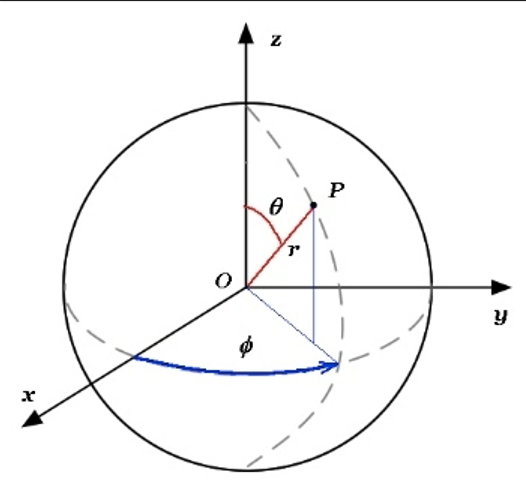
$$(\theta,\phi)\in [0,\pi]*[0,2\pi]$$.
$$x(\theta,\phi)={{Rsin\theta cos\phi}}$$
$$y(\theta, \phi)={{Rsin\theta sin\phi}}$$
$$z(\theta, \phi)={{Rcos\theta}}$$
\(\phi\): Longitude
\(\theta\): colatitude
Bornage des variables des coordonnées sphériques
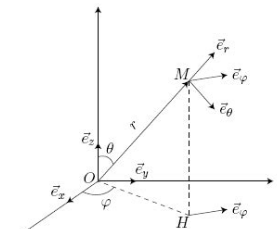
- \(0\leq r\leq \infty\)
- \(0\leq \theta \leq {{\pi}}\)
- \(0\leq \varphi\leq {{2\pi}}\)
Variation élémentaire
Variation élémentaire des coordonnées sphériques

$$d\vec r={{d\vec l_r+d\vec l_\theta + d\vec l_\varphi}}$$
Avec:- \(d\vec l_r={{dr.\vec u_r}}\)
- \(d\vec l_\theta={{rd\theta.\vec u_\theta}}\)
- \(d\vec l_\varphi={{r\sin(\theta)d\varphi.\vec u_\varphi}}\)
Surface infinitésimal
La surface élémentaire est définie par:
$$d\vec S= d\vec l_\theta\wedge d\vec l_\varphi$$
On reconnait la formule de l'aire d'un parallélogramme
Volume élémentaire
Le volume élémentaire est définie par:
$$dV=dS.dr$$
Avec:- \(dS\): la surface élémentaire
- \(dr\): la variation de la coordonnée \(r\)


